¿Cuáles son las 3 alturas de un triángulo?
Las 3 alturas de un triángulo son los segmentos de rectas perpendiculares comprendidas entre el vértice y el lado opuesto de ese, los tres (3) segmentos de las alturas concurren en un punto llamado ortocentro.
¿Cómo trazar las 3 alturas de un triángulo?
Para trazar ahora las 3 alturas de un triángulo necesitaremos tener a la mano una regla y una escuadra. Porque con la escuadra lograremos crear la perpendicularidad (90º) que se requiere.
Primeramente, necesitaremos colocar la regla en el lado opuesto al vértice que vamos a calcular y con la escuadra superpuesta a la regla formando un ángulo de 90º entre el vértice y el lado opuesto.
Imagen
Proceso para calcular las 3 alturas de un triángulo
Ejemplo en un triángulo rectángulo
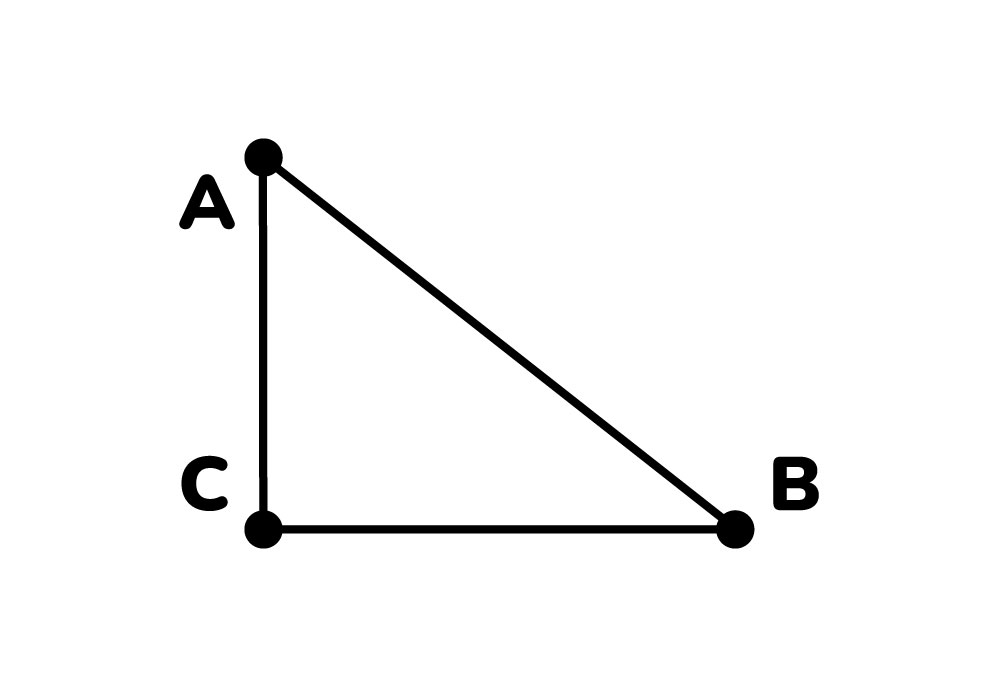
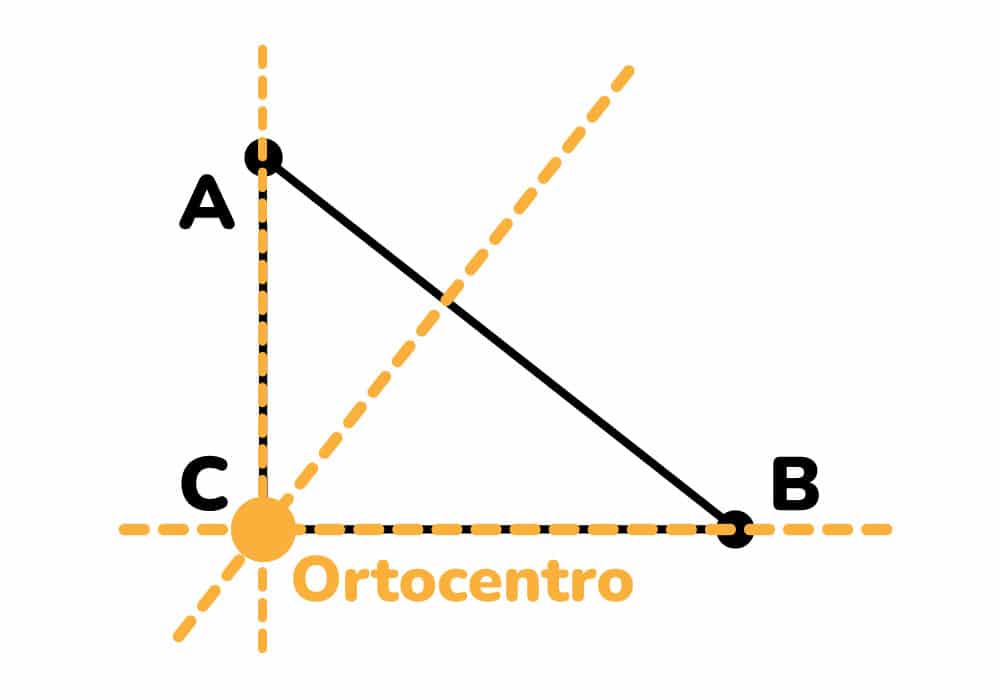
Comenzamos identificando el vértice A, luego trazamos el segmento perpendicular que va desde el vértice A hasta el lado opuesto.
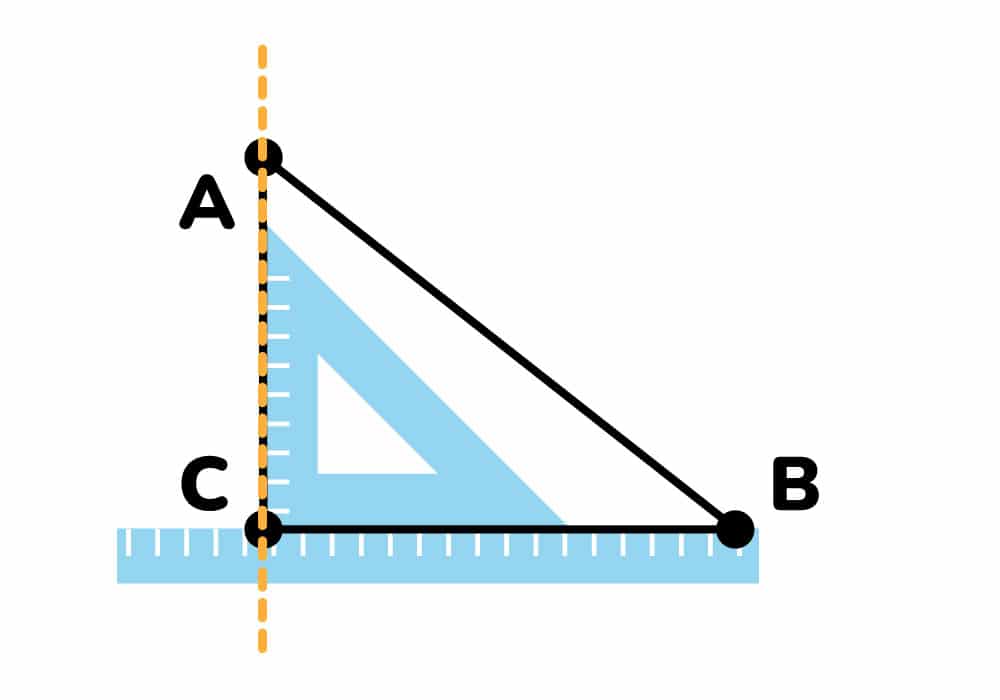
Luego, calculamos la altura del vértice B, haciendo el mismo procedimiento.
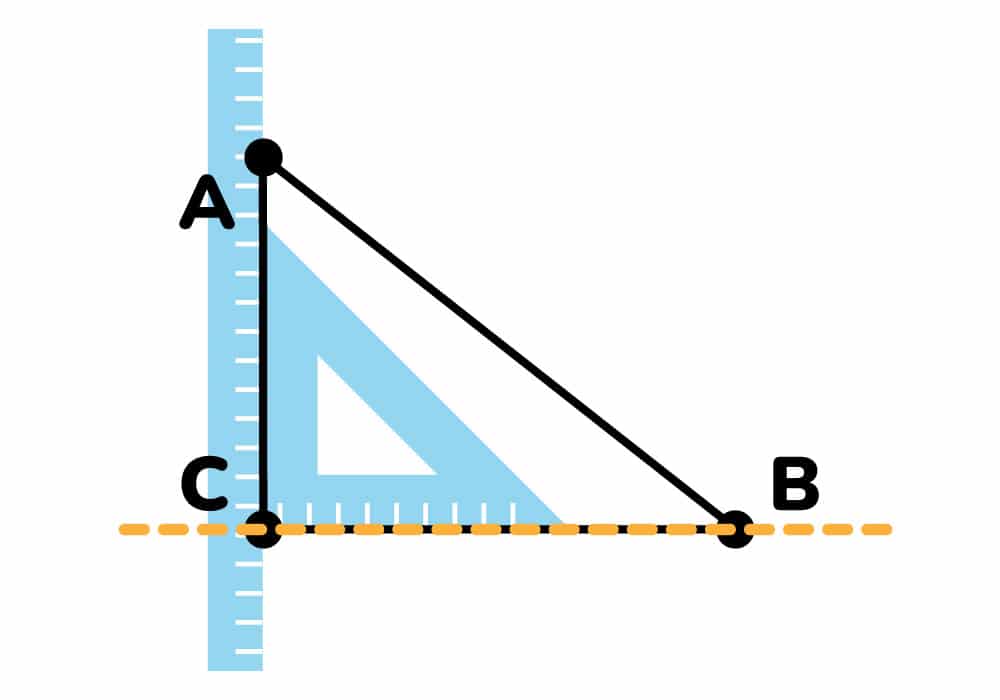
Finalmente, trazamos la altura del vértice C.
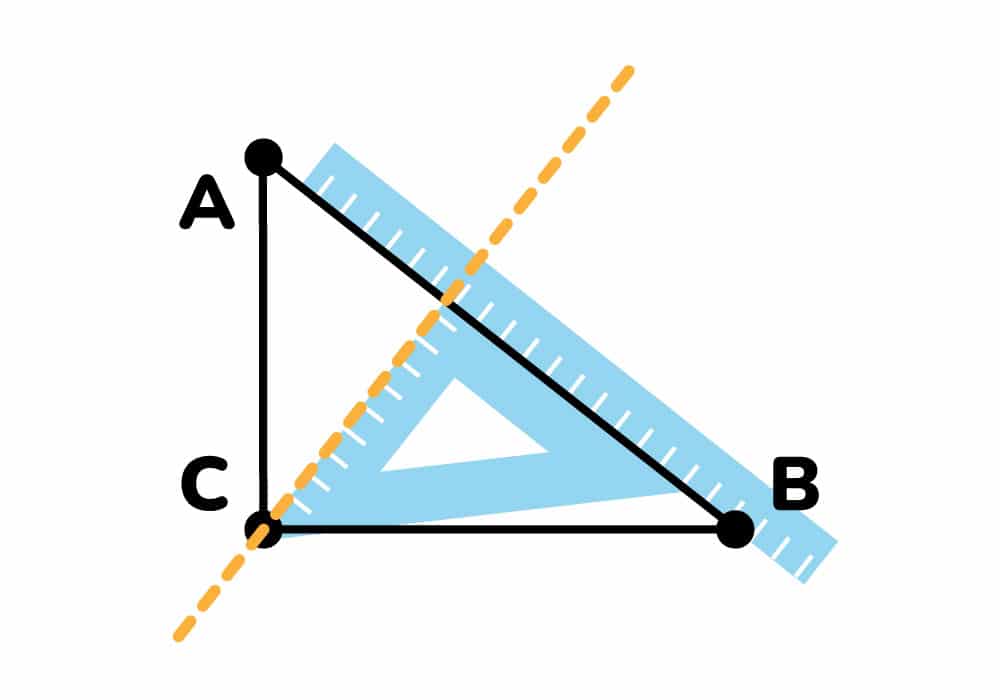
Casualmente en un triángulo rectángulo el punto donde concurren las 3 alturas (ortocentro) está ubicado en el ángulo recto, que en este caso es el vértice C
Ejemplo en un triángulo obtusángulo
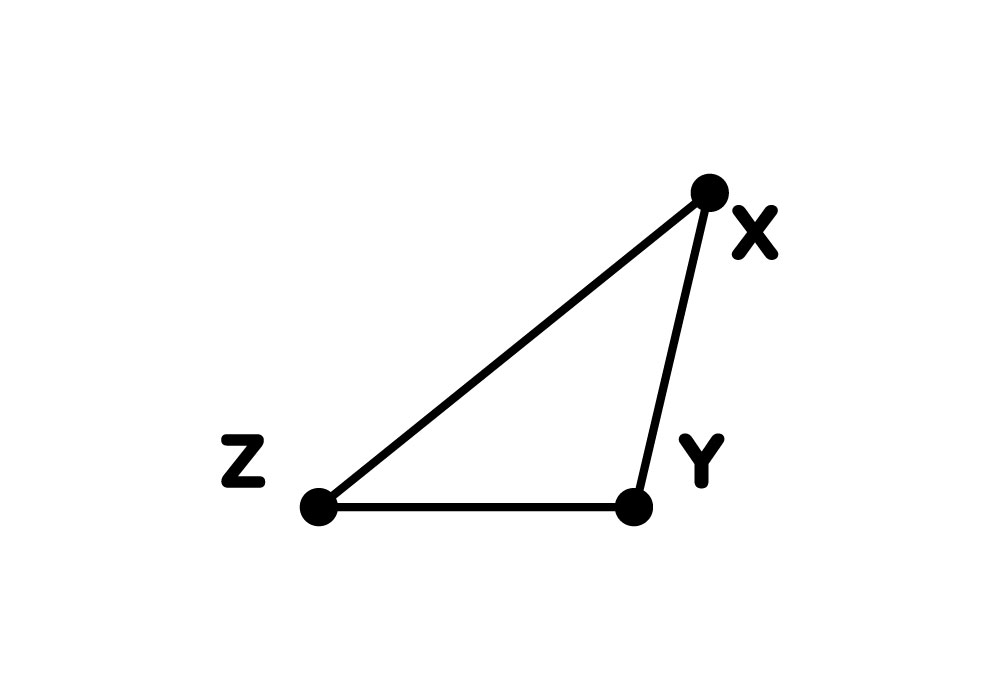
Para trazar las alturas en este tipo de triángulo debemos prolongar los lados que forman el ángulo obtuso
Tramos el vértice X
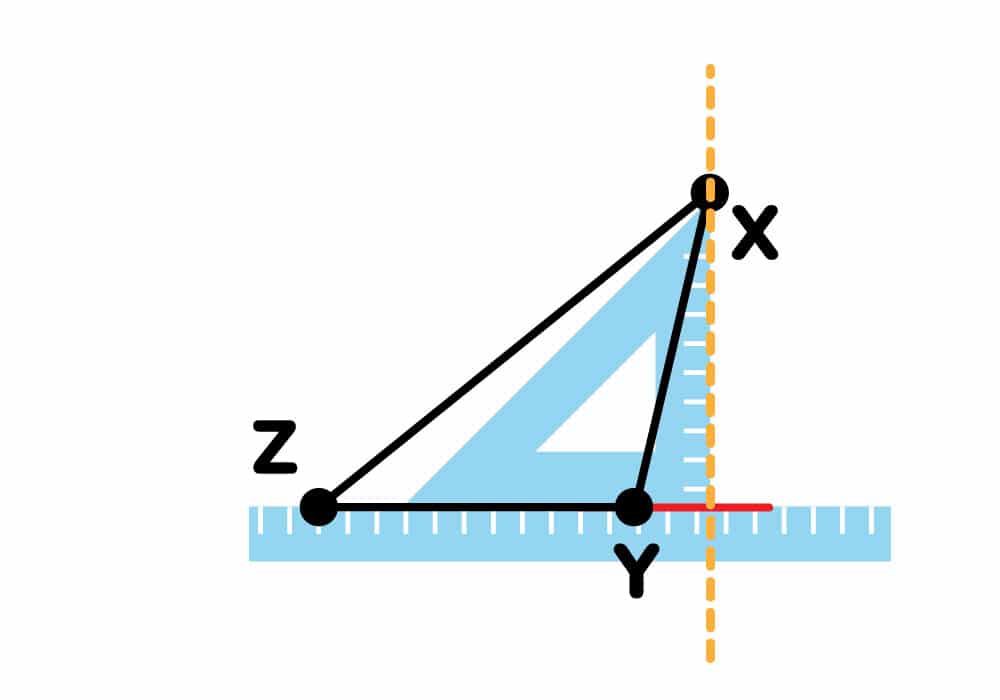
Trazamos el vértice Y
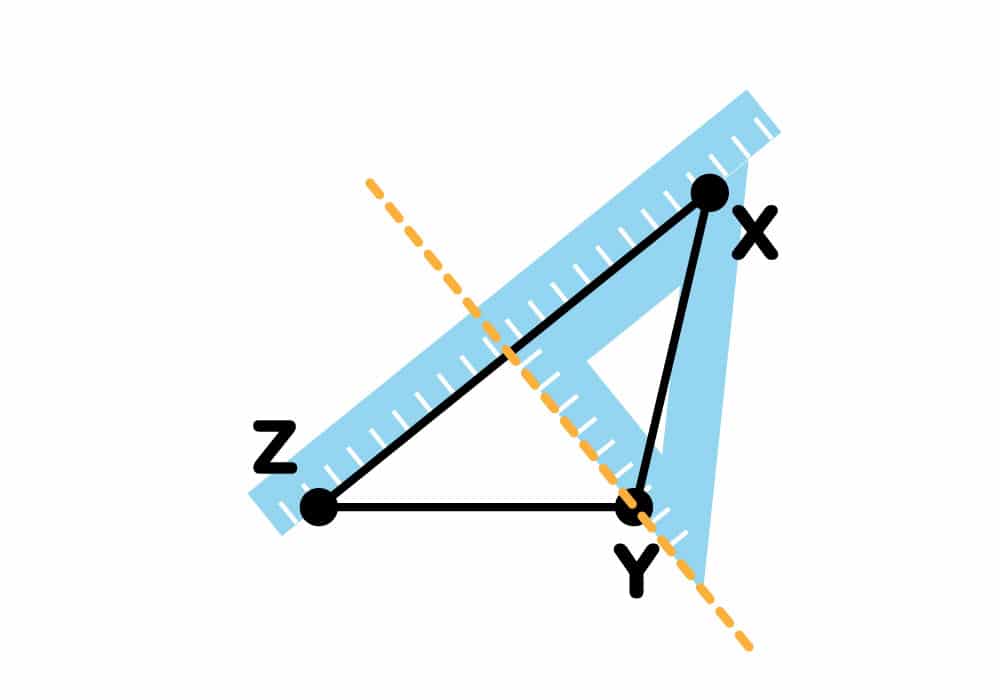
Trazamos el vértice Z
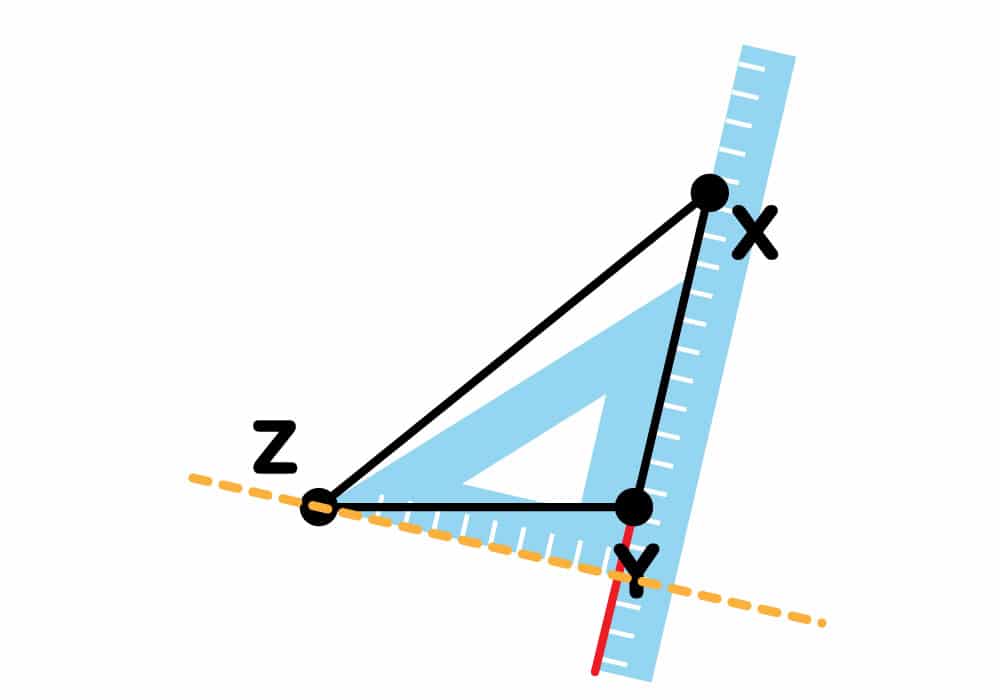
Al trazar las alturas en este tipo de triángulos podemos observar que el ortocentro quede fuera del triángulo.
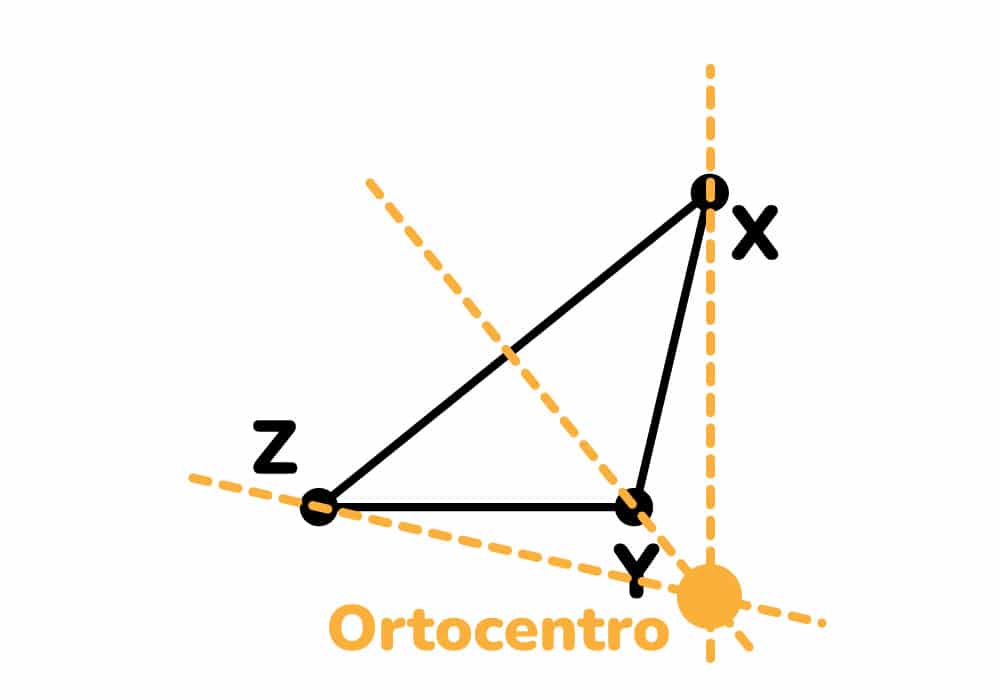
Por todo lo anterior podemos deducir que todo triangulo tiene 3 vértices y por ende tiene 3 alturas, el punto donde se interceptan estos segmentos se llama ortocentro. Particularmente en un triángulo rectángulo este punto se ubica en su ángulo recto, en el obtusángulo este mismo queda fuera del triángulo.

