¿Qué es un prisma rectangular?
Para definir un prisma rectangular primeramente tenemos que saber que un prisma, es un poliedro, este es una figura tridimensional que dos de sus caras son paralelas e iguales llamadas base y el resto de sus caras son rectángulos.
En el caso de prisma rectangular, las dos caras base son de forma rectangular y el resto de las caras también lo son, como es mencionado anteriormente. Estos también son llamados cuboides o poliedros.
Hay dos tipos de estos prismas, los que todos sus ángulos tienen 90º a los cuales se les llama prismas rectangulares rectos y los que su eje principal no es perpendicular a base, los cuales son llamados prismas rectangulares oblicuos.
En la vida cotidiana podemos ver el uso de prismas rectangulares en varios elementos muy comunes, como lo son las cajas de zapatos.
También te puede interesar:
Características de los prismas rectangulares
- Tienen 2 bases rectangulares
- Están formados por 6 caras rectangulares, 2 que son sus bases y 4 caras laterales.
- Todas sus caras paralelas son iguales.
- Está formado por 8 vértices, que son los puntos donde confluyen tres caras del prisma.
- Tienen 12 aristas, estos mismos son los segmentos que donde concuerdan las caras.
¿Cómo calcular el volumen de un prisma rectangular?
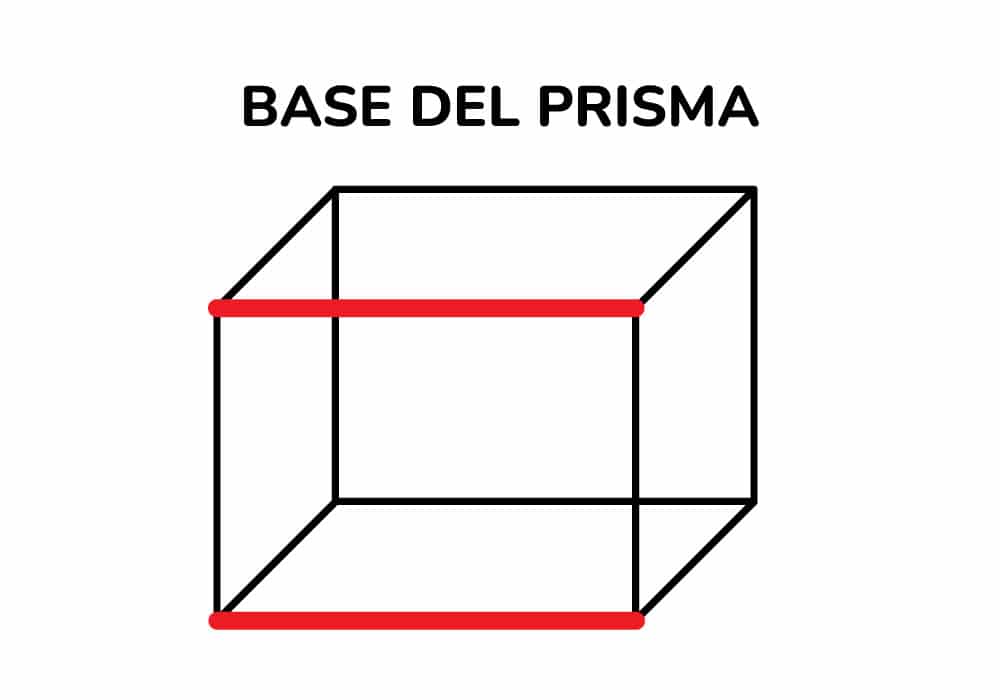
Para calcular el volumen debemos conocer las medidas de la base, altura y el ancho. Comenzamos por ubicar la base que es el lado más largo del prisma y se encuentra en la parte superior o inferior de este.
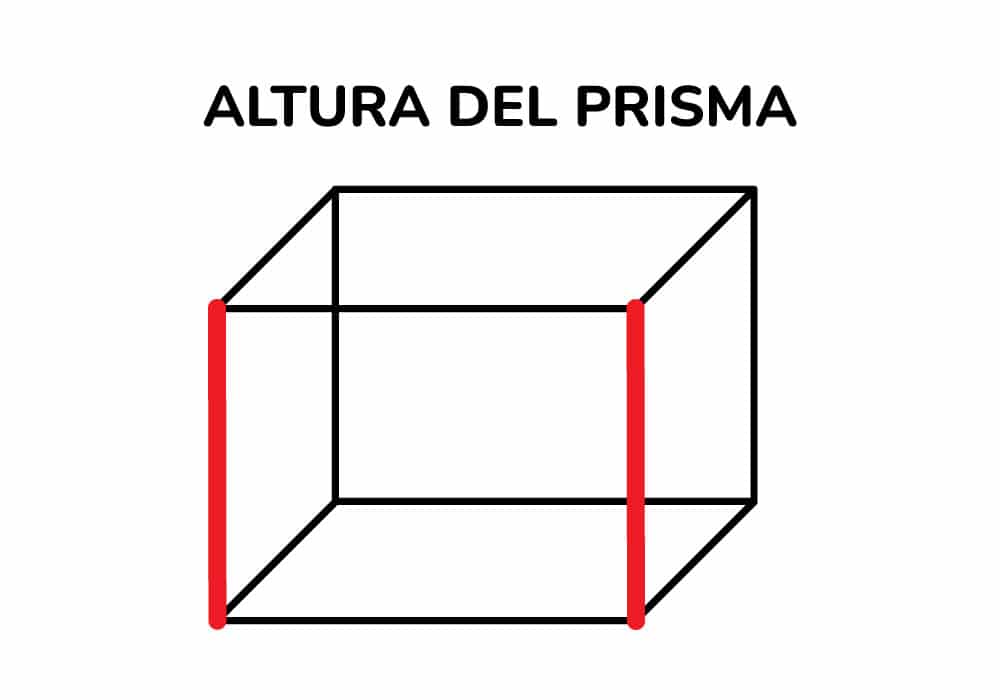
Ahora procedemos a ubicar la altura del prisma rectangular, es la parte del prisma que se eleva, lo que hace que se esté se transforme en una figura tridimensional.
Por último, identificamos el ancho del prisma, que es el lado más corto y también está ubicado en la parte superior o inferior del mismo.
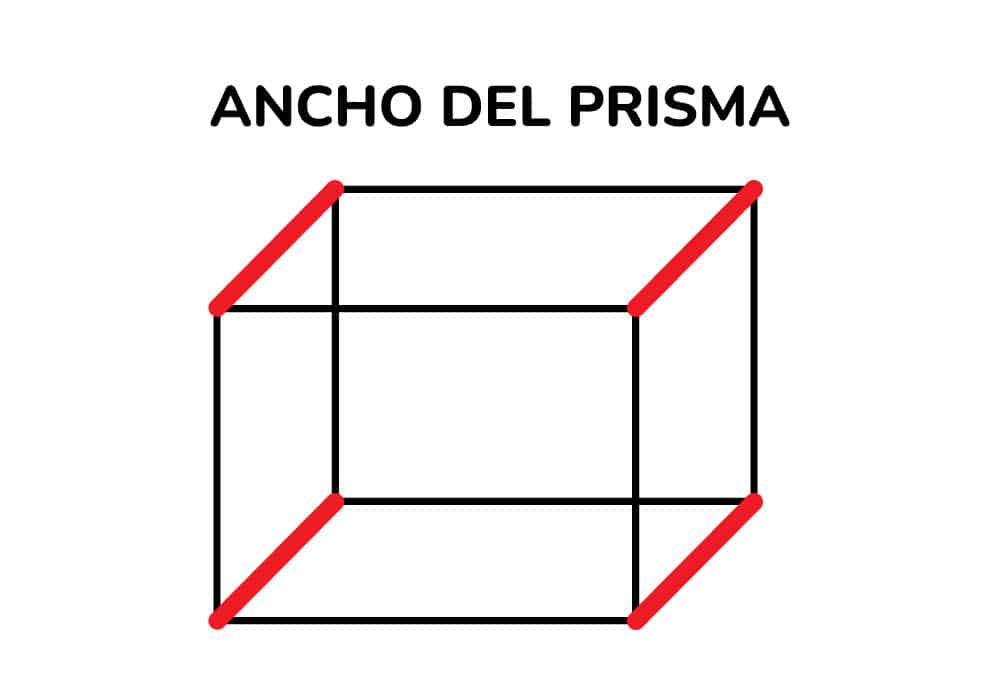
Una vez identificada la base, altura y el ancho, procedemos a aplicar la fórmula para calcular el volumen del prisma rectangular, la cual está determinada de la siguiente manera:
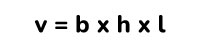
- v= Volumen del prisma.
- l = Longitud del ancho del prisma.
- h = Longitud del prisma.
- b = Longitud de la base del prisma.
Veamos unos ejemplos donde aplicaremos dicha fórmula:
Ejercicio 1:
Calcular el volumen del siguiente prisma rectangular, cuyas medidas son:
B = 8 cm, L = 3 cm, H = 2 cm.
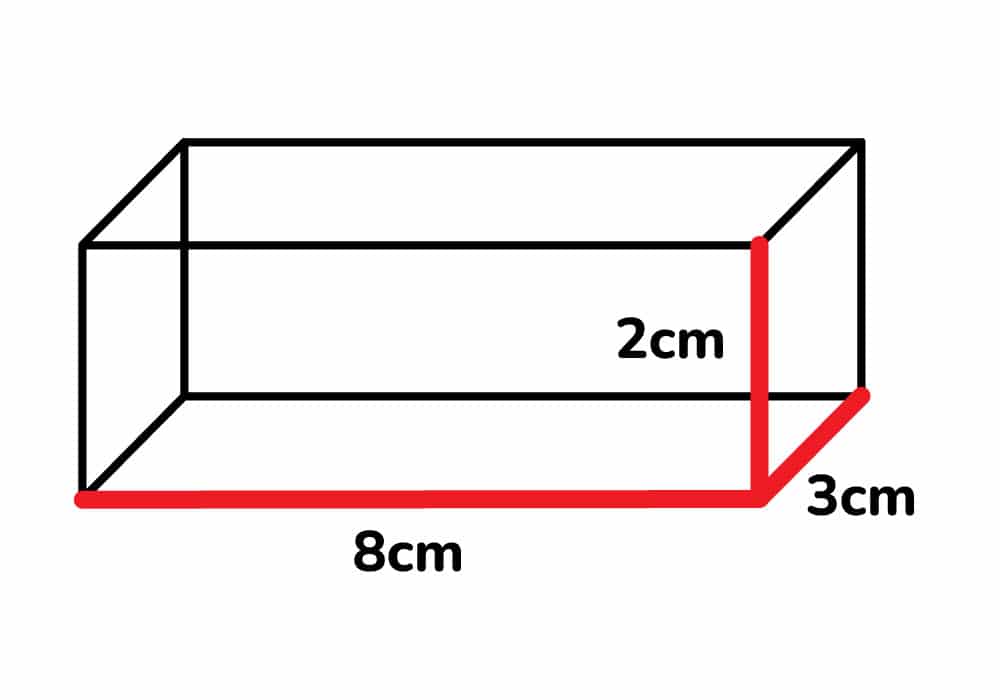
Solución:
Cómo nos dan los 3 datos que necesitamos para calcular el volumen, solo debemos aplicar la fórmula.
v = b x h x l
v = 8 x 2 x 3
v = 48 cm3
Nota: Se colocan cm3 ya que estamos calculando el volumen y trabajamos en un espacio tridimensional, indiferentemente en las medidas que se esté trabajando al final del cálculo la debemos representar en unidades cúbicas.
Ejercicio 2:
Cuál es la base de un prisma rectangular cuyo volumen es de 36 cm3, una altura de 4 cm y un ancho de 2 cm.
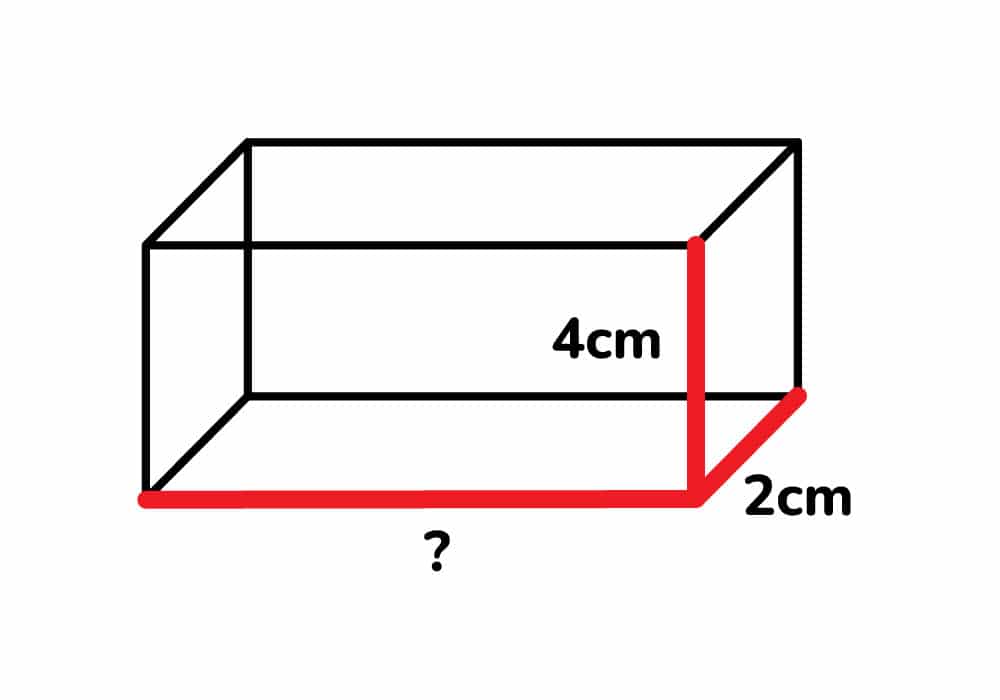
Solución:
En este caso vamos a despejar la base de la fórmula del volumen.
v = b x h x l
36cm3 = b x 4cm x 2cm
36 = b x 8
b = 36/8
b = 4.5cm
La base o el largo del prisma rectangular es de 4,5cm.
¿Cómo calcular el área de un prisma rectangular?
Para calcular el área se tiene que conocer las longitudes de la base, alto y ancho del mismo.
Vamos a realizar dos cálculos, el primero de ellos es calcular el área de la base y el segundo cálculo es el área de la altura o los laterales.
El área de la base se calcula multiplicando la base por el ancho del prisma, este resultado se multiplica por dos, ya que tenemos la parte superior e inferior del prisma rectangular.
Área de la base = base x ancho
Ab = b x l
El área de la altura o los laterales se calcula multiplicando la altura por el ancho del prisma rectangular, luego este resultado es multiplicado por 2, puesto que tiene 2 caras laterales idénticas.
Área de la altura = altura x ancho
Ah = h x l
El área del ancho se calcula multiplicando la longitud de la base por la longitud de la altura del mismo.
Área del ancho = base x altura
Al = b x h
Una vez calculadas estas dos áreas, procedemos a sumarlos, obteniendo así el área total del prisma rectangular. Todo este proceso queda resumido en la siguiente fórmula.
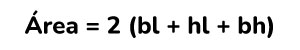
Ejercicio 1:
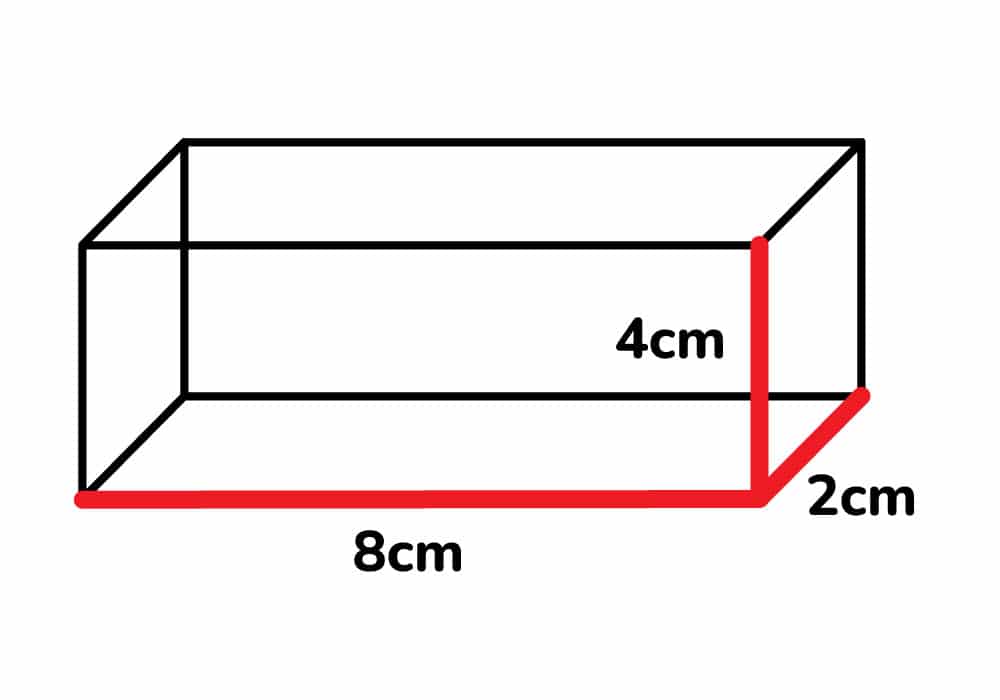
Calcular el área del prisma rectangular cuyas medidas son:
b = 8cm, h = 4cm y l = 2cm
Solución:
Área = 2 (8×2 + 4×2 + 8×4)
Área = 2 (16 + 8 +32)
Área = 2 x 56
Área = 112 cm
¿Cómo calcular la diagonal de un prisma rectangular?
La diagonal de un prisma es una línea recta que va desde un vértice de su base superior hasta el vértice opuesto de la base inferior.
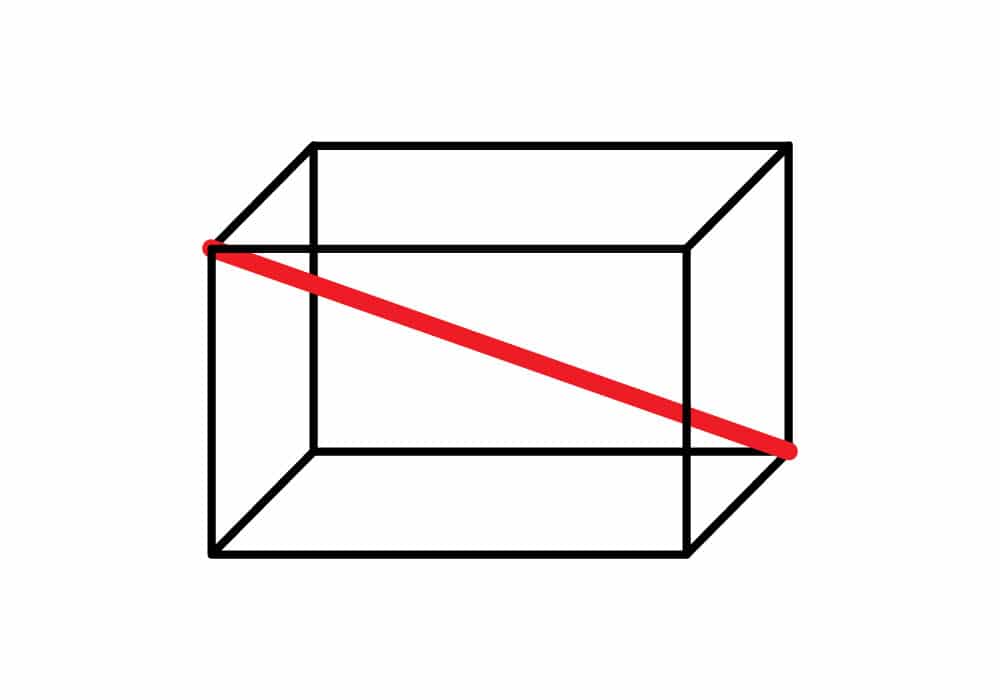
Para calcular la longitud de la diagonal vamos a utilizar el teorema de Pitágoras en sus 3 dimensiones, por lo que necesitamos saber las longitudes de la base, altura y ancho del prisma rectangular. Quedando la siguiente fórmula:
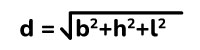
- d= Diagonal del prisma.
- l = Longitud del ancho del prisma.
- h = Longitud del prisma.
- b = Longitud de la base del prisma.
Ejercicio 1:
Calcula la diagonal del siguiente prisma rectangular, el cual tiene 9cm de base, 6cm de ancho y 4cm de altura.
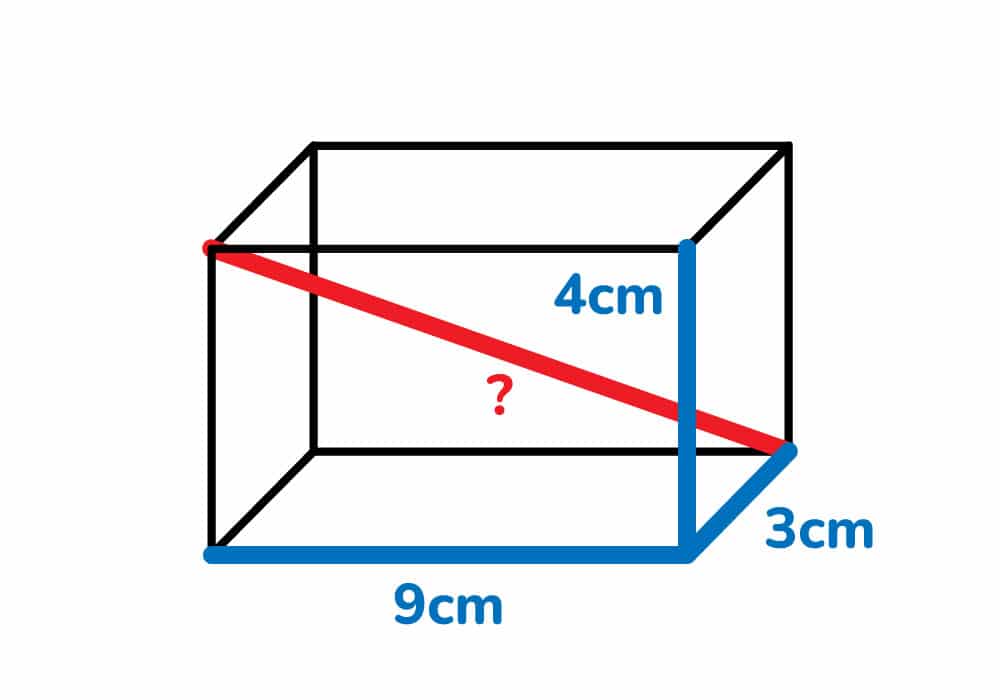
Solución:
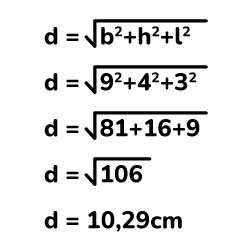
La diagonal del prisma rectangular tiene una longitud de 10,29cm
Ejercicio 2:
Dado el siguiente prisma que tiene como base 24cm, altura de 8cm y un ancho de 13cm ¿Cuánto mide la diagonal del prisma?
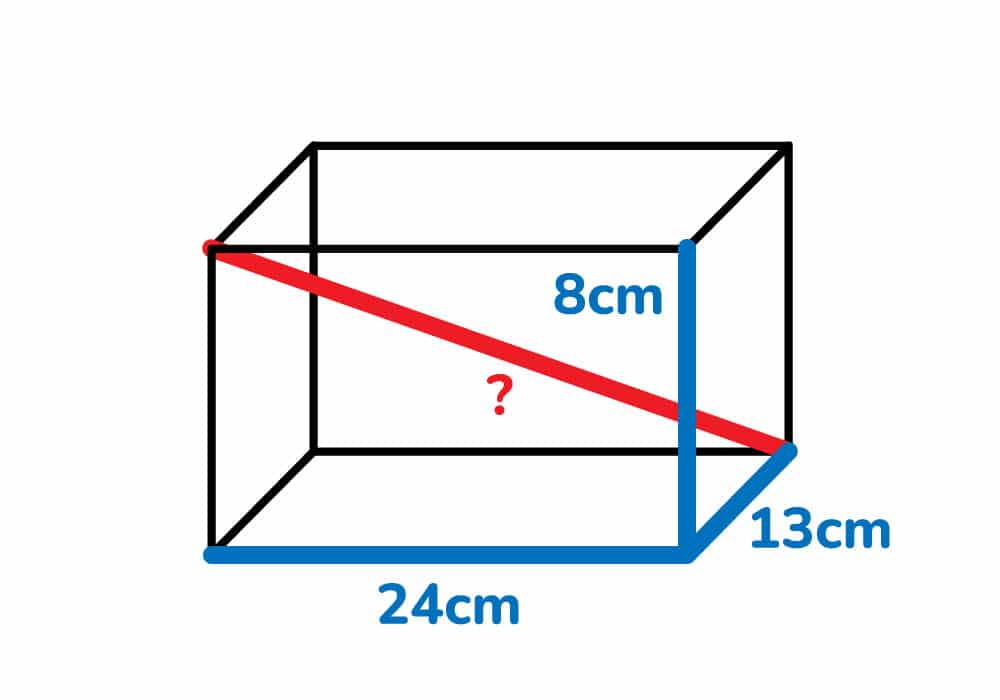
Solución:
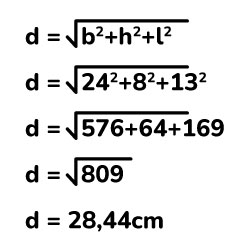
La diagonal del prisma rectangular tiene una longitud de 28,44cm

Buen día! Necesito ayuda! debo responder las siguientes preguntas y no entiendo!!
a-¿Cuántas veces crece el volumen de un prisma rectangular cuando todas las aristas se duplican? ¿Y si solo se duplica el largo y ancho del prisma? ¿Y si sólo se duplica la altura?
b.- ¿Cómo tiene que modificarse el ancho de un prisma si el largo se duplica y la altura se mantiene fija, para que el volumen sea constante? ¿y si el largo se triplica?
c.-¿Qué tipo de relación de proporcionalidad puede establecerse entre la medida de la altura y el volumen del prisma si la superficie de la base permanece constante?
d.- ¿Si se duplican las medidas del largo y del ancho de la base, ¿qué debería suceder con la altura del prisma para que el volumen permanezca constante?