La suma algebraica es la como dice su nombre la suma y resta de términos, estos términos pueden ser términos independientes o dependientes, también se puede aplicar este tipo de propiedad para los monomios, binomios, trinomios y polinomios.
Un ejemplo sencillo de este tipo de suma es la de términos independientes en la cual existen varias formas de resolver, pero el más común es la agrupación de los términos de igual signo para posteriormente realizar la resta de estos dejando el signo del mayor término que tenga la suma.
Ejemplo:
![]()
El primer paso es la agrupación de los términos del mismo signo y se coloca el signo de suma entre ambas agrupaciones lo cual no altera el signo de estas:
![]()
Se realiza la suma de los términos del mismo signo:
![]()
Posteriormente se la suma de las dos agrupaciones dejando el signo del término más grande.
![]()
Suma algebraica de términos semejantes y su simplificación
Para la realización de la suma algebraica en monomio, binomio, trinomio y polinomio es necesario tener conocimiento acerca del término semejante. El término semejante es aquel que posee la misma variable o la misma parte literal, esto quiere decir que posee la misma letra o letras que acompañan el coeficiente.
Para simplificar o reducir los términos semejantes es necesario agrupar estos y solo sumar o restar los coeficientes que los acompañan según sea el signo que poseen.
Ejemplo:
![]() y
y ![]()
Se realiza de los dos términos.
![]()
El término semejante en esta suma algebraica es x, por lo tanto, se toma el valor de esta aparte y se suman los coeficientes:
![]()
Obteniendo como resultado:
![]()
En este caso, la solución de este problema matemático es sencillo debido a que es la suma de dos monomios solamente.
Para la solución de binomios, trinomios y polinomios se tiene que tomar en cuenta este término semejante ya que al no tener en la suma algún término que sea semejante este queda apartado de la suma con el signo que el posee.
Comenzaremos por explicar cuando la suma de estos tiene términos la misma cantidad de términos semejantes.
![]() y
y ![]()
Como anteriormente se explicó se agrupan las variables o los literales y se suman algebraicamente:
![]()
![]()
Una vez realizado este procedimiento se suma los coeficientes y se obtiene el resultado:
![]()
El siguiente ejemplo es cuando existen términos semejantes y otros que no tienen términos semejantes:
![]() y
y ![]()
En este caso, se agrupan los términos de igual literal o variable y se suman los coeficientes, quedando fuera de esta suma los términos que no poseen semejantes:
![]()
![]()
![]()
Se realizan las sumas y se obtiene el resultado:
![]()
Una manera práctica de realizar este tipo de ejercicios es de la manera que se enseña en la educación básica para la realización de suma de números enteros. Se tienen los siguientes polinomios:
![]() y
y ![]()
Se colocan los términos semejantes uno abajo del otro:
![]()
Suma algebraica de fracciones
También existe la suma algebraica de fracciones, en las cuales se utilizan los métodos de acuerdo a su igualdad en el denominador o diferencia en el denominador.
Como ejemplo básico de suma algebraica de fracciones utilizaremos la que tienen igual denominador. Al poseer igual denominador se deja el denominador igual y se suman algebraicamente los numeradores.
Se tienen los siguientes polinomios:
![]() y
y ![]()
Se utilizará el método tipo tabla para la realización de este ejercicio:
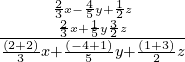
Y se obtiene como resultado el siguiente polinomio:
![]()
Se simplifica la fracción de la variable y el polinomio resultante es:
![]()
Ahora que sabes todo sobre suma algebraica, puedes compartir este articulos para otras personas que lo necesiten y asi nos ayudas para seguir creando contenido.

