Las reglas algebraicas son aquellas que nos permiten sumar, restar, multiplicar, dividir, elevar a una potencia, simplificar las expresiones algebraicas, entre otras cosas, para ello es fundamental algunas reglas.
Estas nos ayudarán a buscar una solución de una manera práctica y con un estudio más profundo y continuo de la materia se realizarán las respuestas más sencillas.
También te puede interesar:
Que es el álgebra y donde se origino
Todo sobre las Expresiones algebraicas
Reglas algebraicas básicas para cualquier tipo de operación
Se pueden tomar estas reglas como las más elementales para la resolución de operaciones matemáticas con expresiones algebraicas, están son las siguientes:
Regla de los signos.
Esta regla se utiliza cuando se realiza la multiplicación de dos términos algebraicos, estos pueden ser signo positivo o signo negativo.
En caso de que los signos que se multipliquen sean iguales los dos positivos o los dos negativos, el signo resultante será positivo y de ser los signos opuestos en la multiplicación de los términos de la expresión algebraica, el signo resultante será negativo.
Cómo se puede visualizar en la siguiente tabla:
![]()
La regla de la potencia
Cuando se posee una multiplicación con potencia de igual base es equivalente, a la misma base y se procede a sumar los exponentes que estas poseen. Un ejemplo:
![]()
Se realiza en procedimiento dejando la misma base y sumando los exponentes:
![]()
Teniendo como resultado la siguiente expresión:
![]()
La regla de la potencia se utiliza cuando existen números enteros o fracciones en la potencia con la misma base.
En el caso de que se realice una división con variables de la misma base, se procede a dejar la misma base y a restar los exponentes de las mismas, como se representa a continuación:
![]()
![]()
![]()
La regla de coeficientes
Esta regla es usada en todas las operaciones realizadas con expresiones algebraicas, ya que en la suma o resta los términos semejantes se puede simplificar dichas expresiones sumando los términos y quedando el signo del número de mayor valor.
Se puede ejemplificar de esta manera:
![]()
Se agrupan los términos semejantes:
![]()
Y se procede a simplificar la expresión sumando los coeficientes de las variables iguales, dando como resultado la siguiente expresión:
![]()
La regla de Ruffini.
Esta regla se utiliza para factorizar los términos de la expresión algebraica, para posteriormente realizar las operaciones matemáticas en los polinomios, siendo muy utilizada cuando estos polinomios son fracciones algebraicas.
Ruffini nos determina que el polinomio no es completo, los términos se completan con el valor de 0. Tomamos el siguiente polinomio:
![]()
Se realiza la factorización por la regla de Ruffini, se colocan todos los coeficientes del polinomio con el mismo signo que poseen:
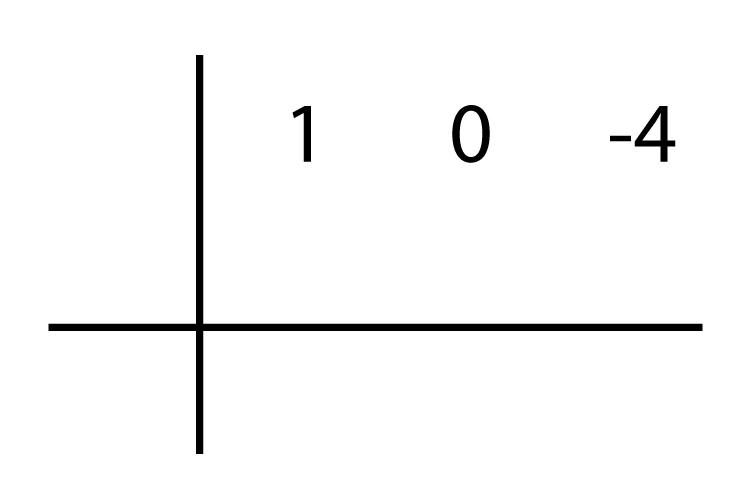
Como no posee la variable x se completa con 0, y se procede a buscar un número que multiplicado por cada uno de los términos de cómo resultado 0 o lo más cercano a cero en el residuo.
La regla nos indica que se baja el primer coeficiente y se coloca el número que nos proporcionará un resultado en el residuo cercano a cero o cero.
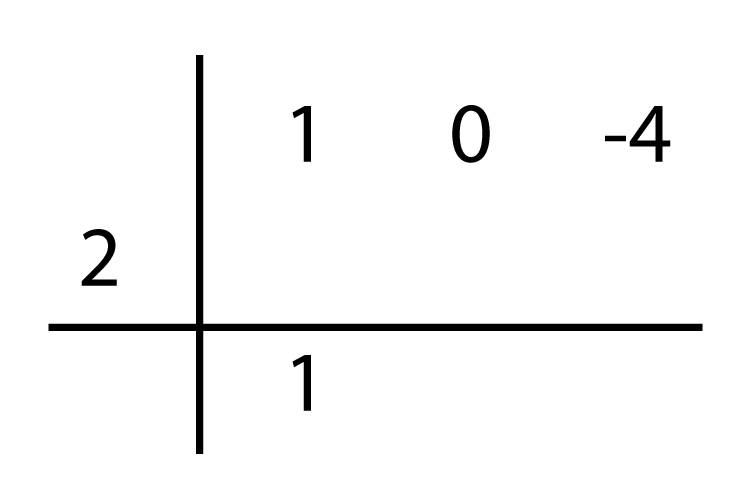
Se procede a multiplicar el valor de 2 por el coeficiente del primer término y se suma algebraicamente por el coeficiente del segundo término.
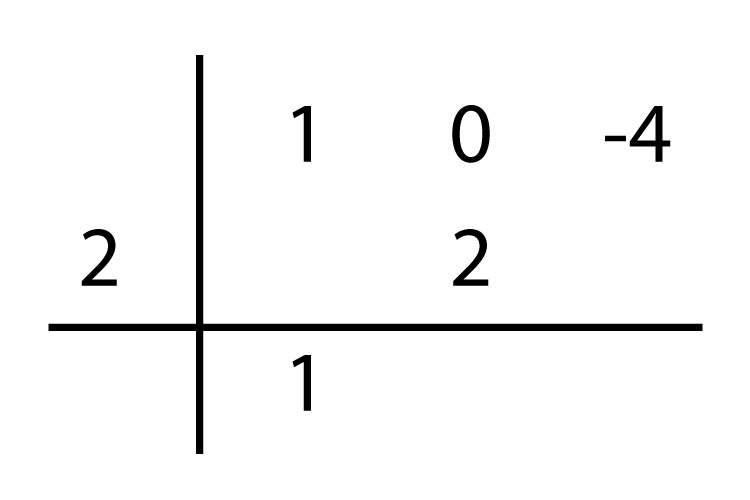
El resultado que se obtiene se vuelve a multiplicar por el valor de 2 y se suma algebraicamente con el coeficiente del tercer término:
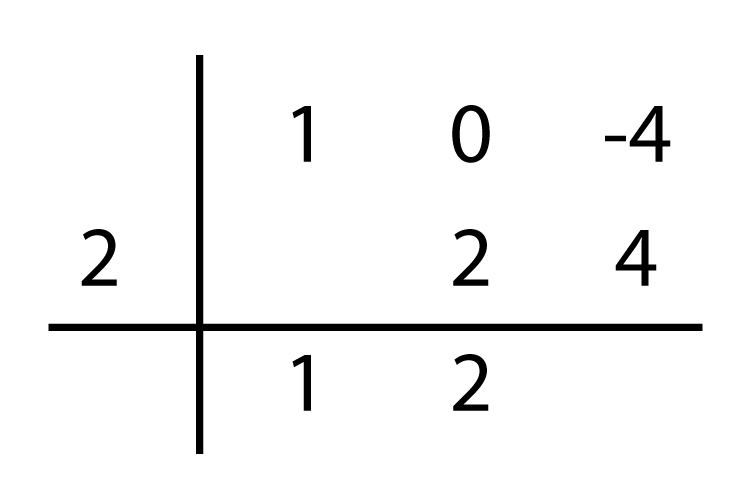
El resto en este caso es 0 lo cual nos simplifica la expresión algebraica.
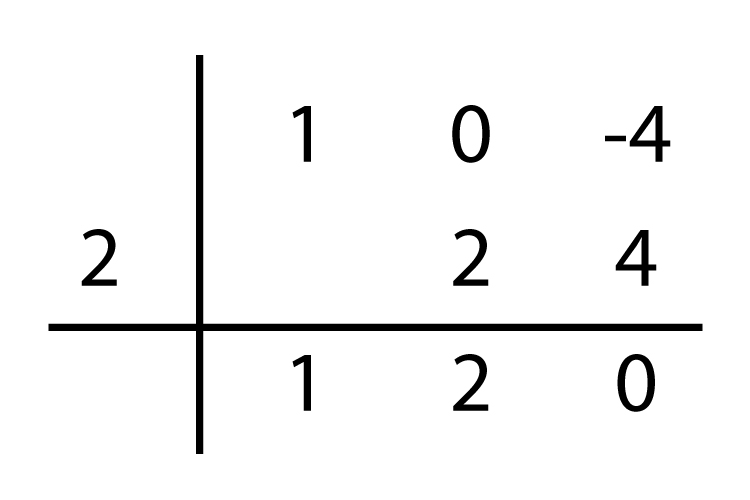
En el caso del valor de divisor se le cambia el signo y los valores resultantes de la operación se mantienen igual, por lo tanto, quedaría expresada la factorización de la siguiente manera:
![]()
Si tienes alguna duda sobre las reglas algebraicas no dudes en escribirme en los comentarios.


Muchas gracias por compartir su material didáctico. Me ha sido de utilidad. Saludos desde Chiapas, México.