Teoría de conjuntos – Definición, símbolos y ejemplos

¿Sabes que es la teoría de conjuntos? Te has puesto a pensar que pasaría si separáramos en grupos todas las cosas que nos rodean, como un grupo formado por todas las frutas del mundo o también podría ser los billetes de todo el mundo.

Todos estos grupos mencionados anteriormente pueden ser divididos o subdivididos en múltiples características, como lo son el tipo, color, tamaño, etc.

Ahora todos los conjuntos obtenidos, ¿Tendrán una propiedad matemática común?

Pues de eso se trata la teoría de conjuntos donde a partir de esos conjuntos y sus elementos se establecen ciertas relaciones y propiedades que son independiente en la realidad concreta.

¿Cómo se define un conjunto?

Matemáticamente, consideramos un conjunto una agrupación de elementos perfectamente definidos, ósea, cuando sabemos exactamente qué elementos pertenecen al conjunto.

Para definir un conjunto utilizamos las llaves {}, donde estás encierran sus elementos o la propiedad que los caracteriza.

También te puede interesar:
Símbolos matemáticos más y menos usados

Los conjuntos pueden estar definidos de dos maneras:

1. Extensión o enumeración: se nombran todos los elementos que forman el conjunto.
2. Comprensión o propiedad: se nombra un enunciado que permita afirmar si cualquier elemento pertenece o no al conjunto.

Ejemplo: dado el conjunto N = {días de la semana}.

Si lo definimos por extensión seria:

N = {lunes, martes, miércoles, jueves, sábado, domingo}

Ahora vamos a definir el conjunto por compresión, quedaría de la siguiente manera:

N = {x|x es día de la semana}

Este conjunto se lee: el conjunto N está formado por los elementos x, tal que x es día de la semana.

Para designar un conjunto utilizamos las letras en mayúscula (N, S, P, T, etc.) y cada elemento lo designamos con las letras minúsculas, su representación gráfica se realiza a través de un diagrama de Venn.

Ejemplo:

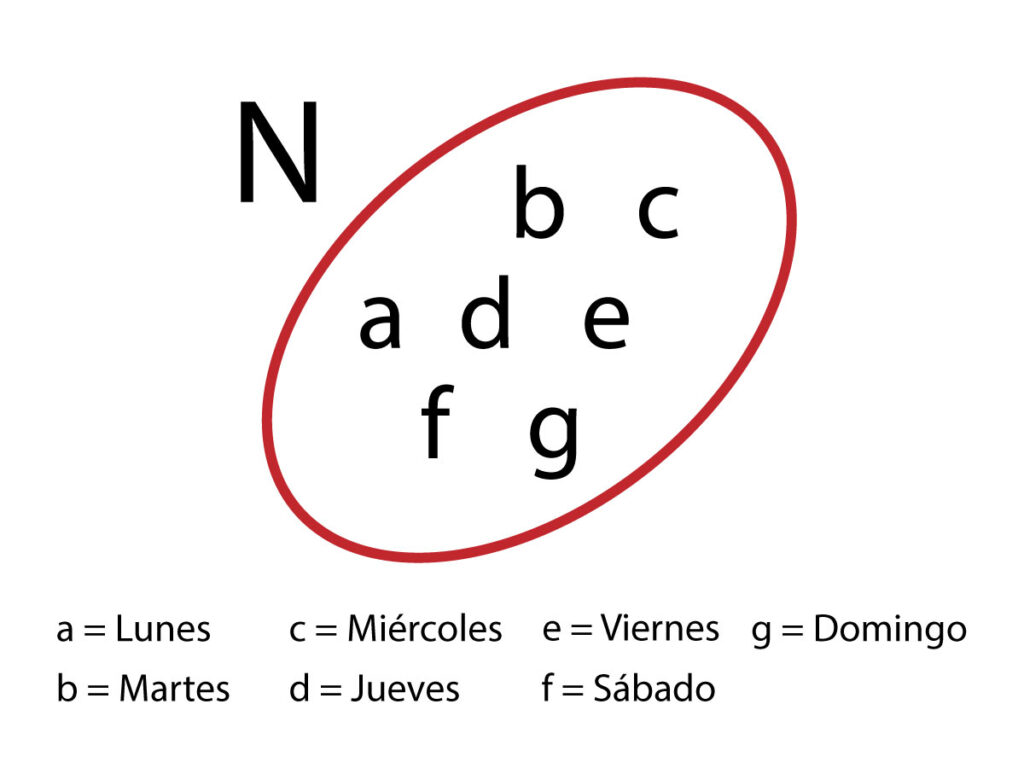
Pertenecía en la teoría de conjuntos

Cuando decimos que un elemento está dentro de un conjunto, nos referimos que dicho elemento pertenece al conjunto, para indicar que pertenece se utiliza el símbolo ∈. Ahora, cuando un elemento no está dentro del conjunto, nos referimos a que el elemento no pertenece al conjunto y para indicarlo utilizamos ∉.

Ejemplo:

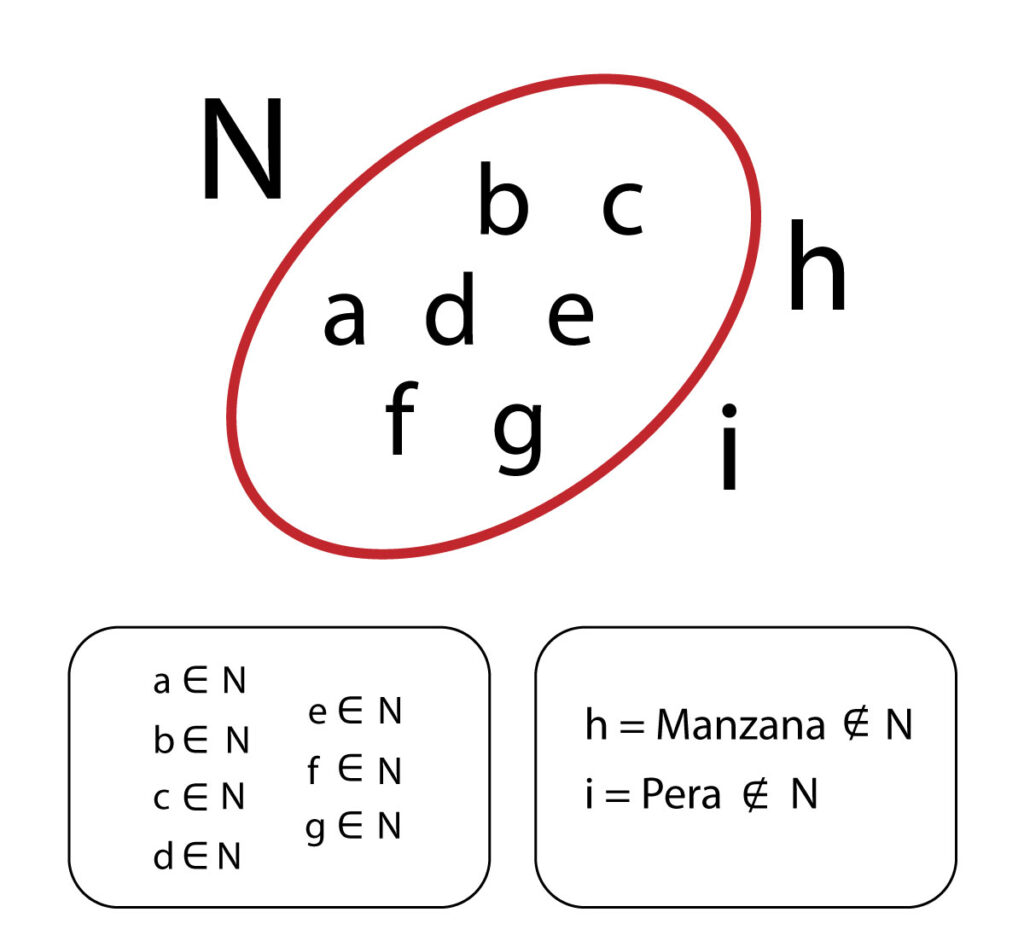
¿Qué es un conjunto infinito?

Los conjuntos infinitos son todos aquellos conjuntos donde es imposible nombrar su último elemento, puesto que siempre se puede nombrar uno más, por ejemplo:

ℕ = {Números naturales}
ℕ = {1, 2, 3, 4, 5, …}

Para indicar que son conjuntos infinitos se cierra la llave después de puntos suspensivos (…) y así señalar que no hay último elemento.

¿Qué es un conjunto finito?

Los conjuntos finitos son todos aquellos conjuntos donde es posible enumerar o nombrar todos sus elementos, si dicho conjunto es un poco extenso se escriben los primeros elementos y luego de puntos suspensivos (…) se coloca el último elemento del conjunto, ejemplo:

B = {los meses del año}
B = {enero, febrero, marzo, …, diciembre}

¿Qué es un conjunto notable?

En la teoría de conjuntos existes 3 tipos de conjuntos notables y son llamados conjuntos vacíos, unitario y universal.

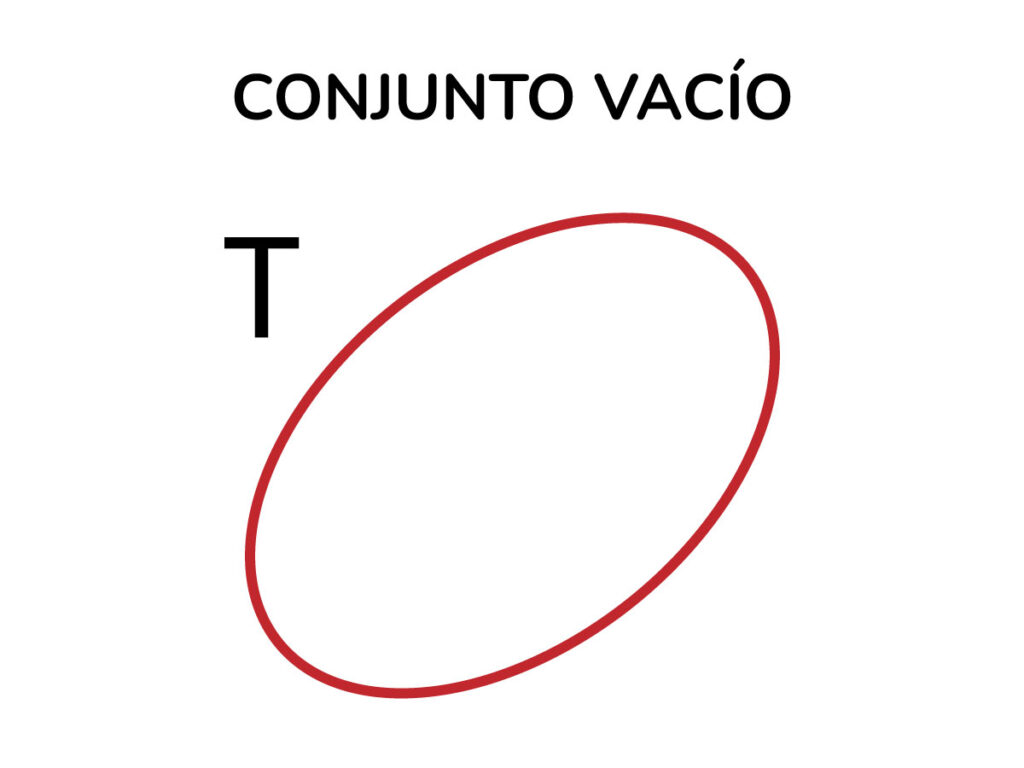
Conjunto vacío

Como su nombre bien lo dice “vacío”, es aquel conjunto que no posee ningún elemento y se denota con el símbolo ø.

Ejemplo:

T = {x|x es un estudiante de la universidad con 3 años de edad}
T = ø

El conjunto T es un conjunto vacío porque en la universidad no se encuentran estudiantes con 3 años de edad.

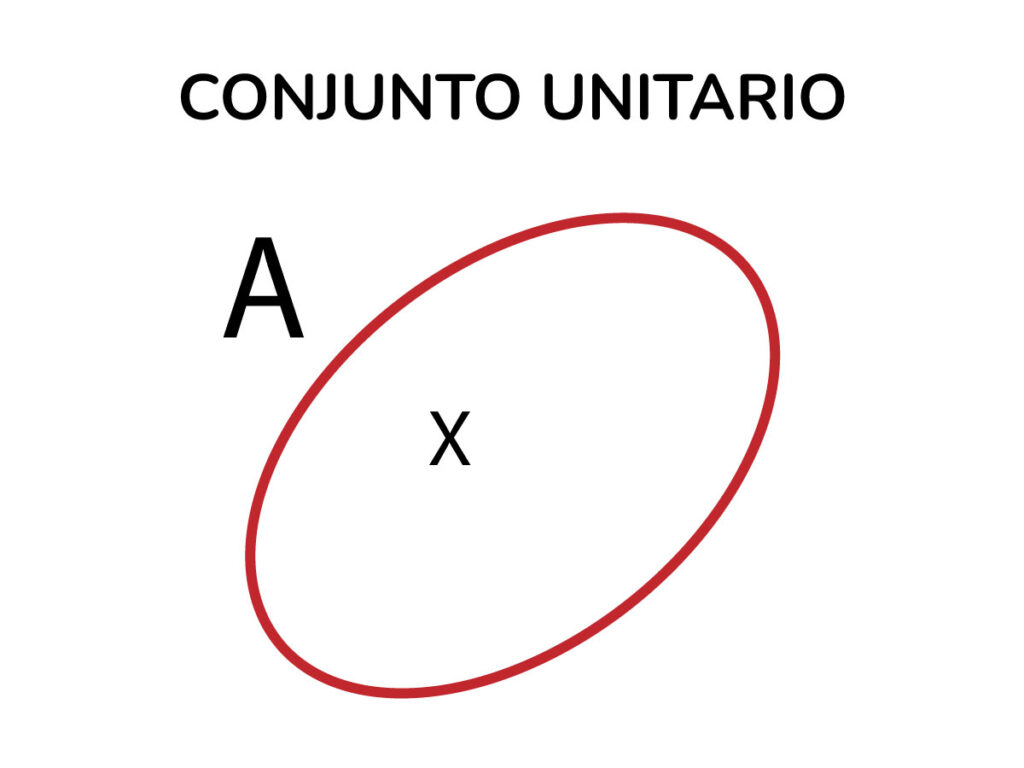
Conjunto unitario

Es aquel que posee un solo elemento

Ejemplo:

A = {x|x es satélite natural de la tierra}
A = {x = luna}

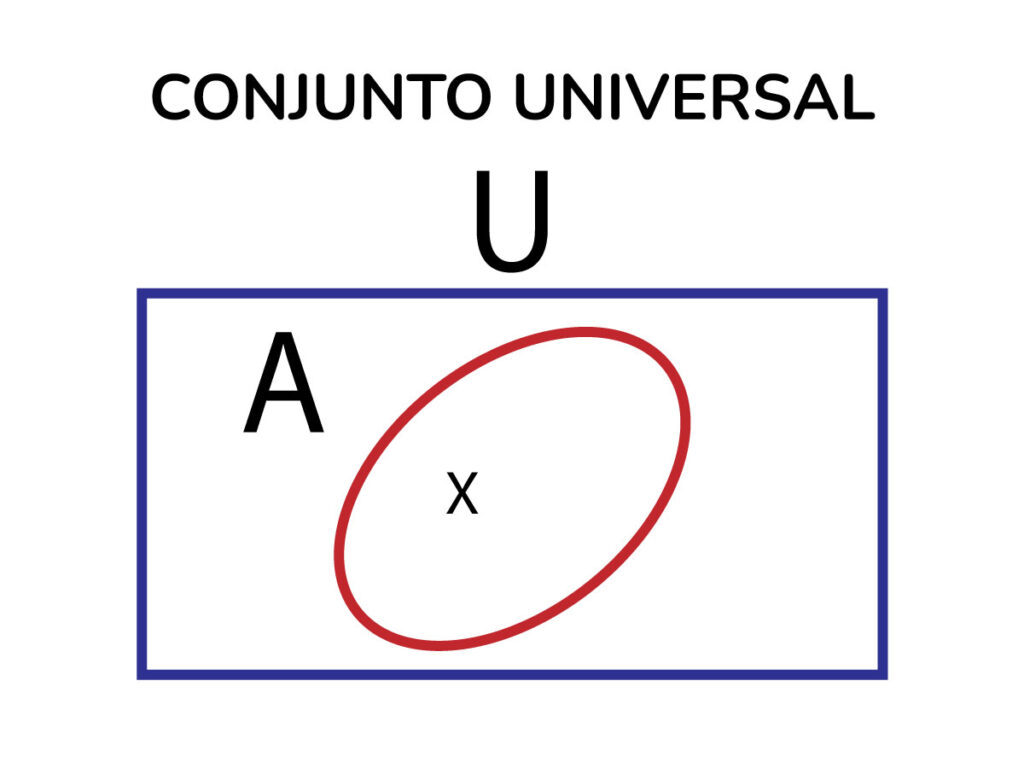
Conjunto Universal

Es el conjunto formado por todos los elementos de un tema de referencia, se simboliza con la letra U y se representan a través de un rectángulo, ejemplo:

Tomemos como el conjunto universo, el conjunto de todos los animales.

U = {x|x es un animal}
A = {x|x es un perro}