¿Qué es una derivada?
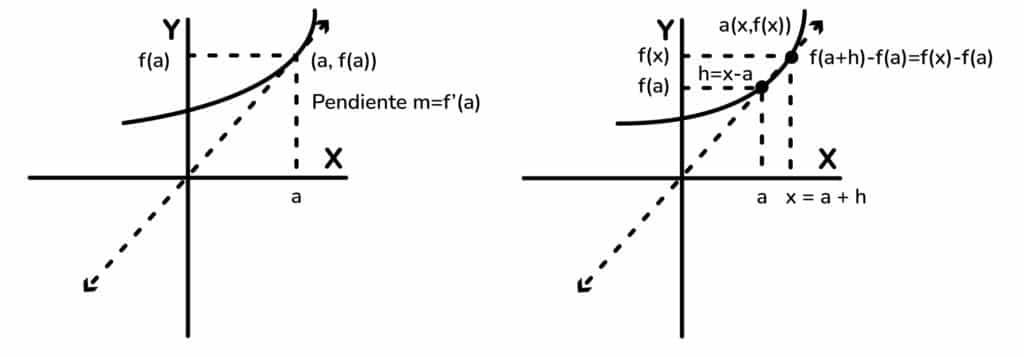
Se utiliza en matemática para el cálculo de respuestas de una función a la que se le están alternando sus valores iniciales, el cual está representada gráficamente como una línea recta superpuesta sobre otra curva (función) y el valor de esta pendiente respecto al eje sobre el cual está siendo evaluada la función recibe el nombre de derivada.
También te puede interesar:
¿Para qué sirve?
Sirven para garantizar u optimizar sistemas que se expresan con funciones más o menos complejas.
Uso de las derivadas en la vida diaria
No solo cumple un papel fundamental en el área de la matemática, sino también en diversas ciencias como la física, mecánica, biología, en el estudio de la medicina y la economía.
Una forma más sencilla de comprenderlas es saber que estas representan razones de cambio, en ingeniería por ejemplo sirve para calcular la variación de la temperatura en un tubo cuando aumenta la presión.
Otro ejemplo sería para calcular cuánto tiempo le durará la batería a un celular en función al cambio de consumo de corriente durante una llamada.
Derivada de una función real
La función f es la función f’ definida por:
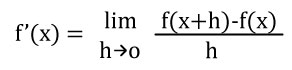
Para todo x donde exista este límite.
Cuando estamos interesados particularmente en el valor de la derivada f’ en x=a reescribimos la definición así:
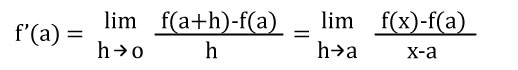
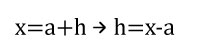
Se observa que x→a cuando h→0 si el límite de la definición existe decimos que la función f es derivable o diferenciable en x=a. el proceso de encontrar la derivada (f’) se llama derivación de f.
Hallemos la derivada por definición de las siguientes funciones:
Ejercicio 1:
En este ejercicio aplicaremos la definición de la derivada mencionada anteriormente.
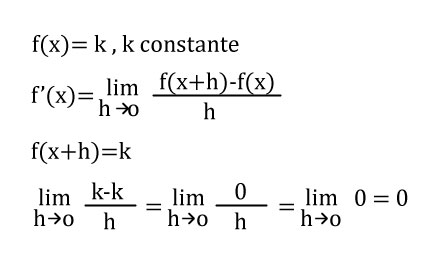
Ejercicio 2:
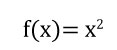
Aplicamos la definición.
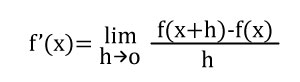
Reescribimos f(x)
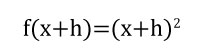
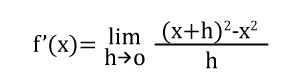
Ahora vamos a desarrollar el producto notable.
(a+b)2 = a2 + 2ab + b2
(x+h)2 = x2 + 2xh + h2
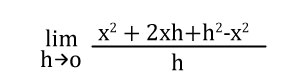
Procedemos a aplicar propiedades en R,
a – a = 0 ; x2 – x2 = 0
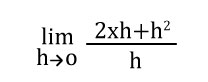
Desarrollamos la propiedad distributiva o factor común, en este caso h.
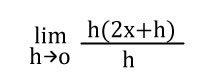
Nuevamente, aplicamos propiedades en R.
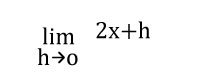
En este paso aplicaremos una de las reglas de derivación.
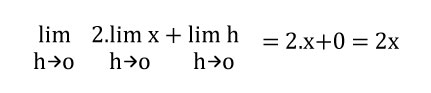
Resolvemos 2 . x + 0
Quedando como resultado 2x.


Necesito más ejemplos que sean difíciles.. Xq los que estan ahí son complejos