El estudio de este conjunto numérico (números enteros) ha sido y es de mucha importancia para la matemática, surge después del conjunto de los números naturales (N). En el principio se utilizaba para representar deudas y ganancias, así mismo para dar respuesta a las temperaturas bajo cero y profundidades con respecto al nivel de mar.
¿Cómo se denotan los números enteros?
Se denotan de la siguiente manera:

Dentro de este conjunto se encuentran los números naturales, el cero (0) y los opuestos o negativos de los naturales
Simbología de los números enteros
Su simbología se debe a la tabla inicial del vocablo Alemán Zahlen (Números). El cero no es ni positivo ni negativo, es el elemento neutro, los números negativos siempre serán menores que los números positivos.
Representación gráfica en la recta numérica
Se disponen en una semirrecta los elementos del conjunto, en el centro de la misma el cero (0), en el lado derecho los enteros positivos y del lado izquierdo los enteros negativos. Cada elemento está a igual distancia y con una única posición en la recta

Valor absoluto en un número entero
El valor absoluto de un número entero es el mismo número positivo, para indicar el valor absoluto de este mismo, se encierra entre dos barras verticales.
|-10| = 10
|10| = 10
Por lo tanto -10 y 10 tienen el mismo valor absoluto que es 10
Operaciones con los números enteros
Para sumar números enteros hay que tener en cuenta si las unidades que se añaden son positivas o negativas.
Ejercicio 1
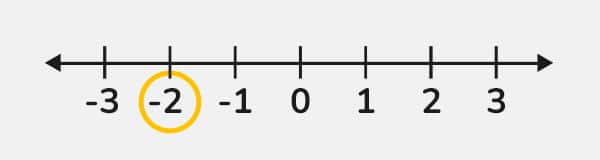
(-2) + (+5)
Representamos el -2 en la recta numérica
Luego le añadimos 5 unidades positivas, 5 unidades a la derecha desde el -2
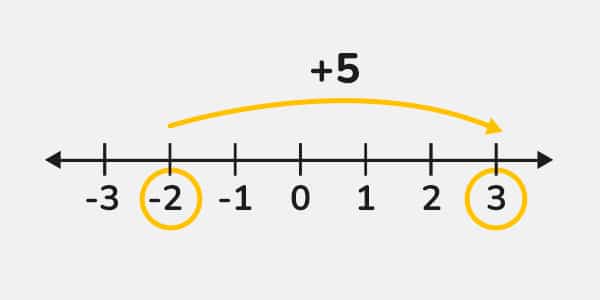
3 es el resultado obtenido de añadir 5 unidades positivas a -2
(-2) + (+5) = 3
Ejercicio 2
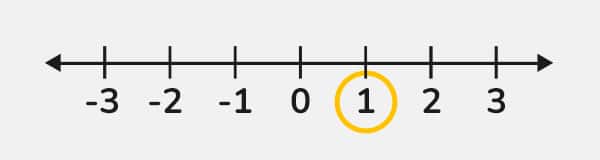
(+1) + (-3)
De igual forma representamos el número 1 en la recta numérica.
Añadimos 3 unidades negativas (-3), se cuentan 3 posiciones hacia el lado izquierdo de la recta.
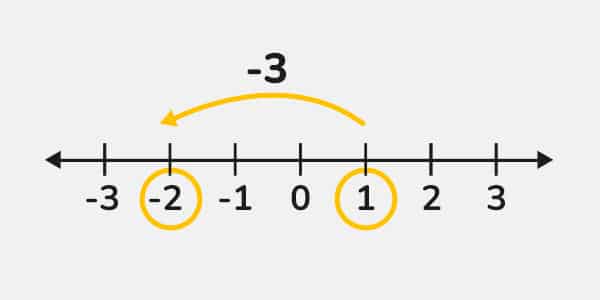
Entonces el resultado es:
(+1) + (-3) = -2
Ejemplo 3
(-5)+(-1)+(-2)=-8
(+10)+(+2)+(+7)=+19
* Cuando los números tienen el mismo signo se suman y se mantiene el signo
Ejemplo 4
(-2)+(+1)+(-3)=-4
(+3)+(+7)+(-2)=+8
Cuando tenemos una suma con números de distintos signos, lo primero que tenemos que hacer es adicionar los números que tengan el mismo y luego restar el número con el signo contrario, se coloca el signo que tenga el número mayor.
Propiedades de los números enteros
Conmutativa:
a+b = b+a
Ejemplo:
(-2) + (+3) = (+3) + (-2)
(+1) = (+1)
Asociativa:
(a+b)+c = a+(b+c)
Ejemplo:
[(-2) + (+3)] + (+5) = (-2) + [(+3) + (+5)]
(+1) + (+5) = (-2) + (+8)
(+6) = (+6)
Elemento neutro
En el conjunto de los números enteros existen un número que al sumarlo con cualquier otro entero da como resultado el mismo número entero, ese elemento neutro en la suma es el cero.
Ejemplo:
- 0 + (-5) = -5
- 0 + (+7) = +7
Multiplicación de números enteros
En la multiplicación de dos o más números enteros, da como resultado otro número entero.
Para multiplicarlos necesitamos de la siguiente tabla de multiplicación de signos:
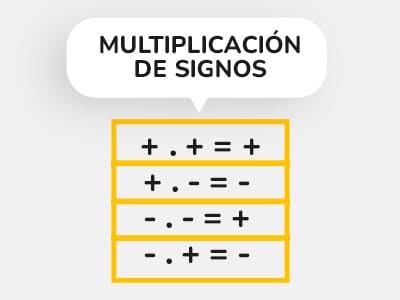
Ejemplo:
- (-2) . (-3) = +6
- (+3) . (+3) = +9
- (-2) . (+2) = -4
- (+5) . (-2) = -10
- (-2) . (-3) . (-1) = -6
- (+2) . (-3) . (-3) = +18
Propiedades de la multiplicación
Conmutativa: a.b=b.a
Ejemplo:
(-3) + (+2) = (+2) . (-3)
(-6) = (-6)
Asociativa: (a.b).c = a.(b.c)
Ejemplo:
[(+2) . (+2)] . (+3) = (+2) . [(+2) . (+3)]
(+4) . (+3) = (+2) . (+6)
(+12) = (+12)
Elemento neutro: El producto de los números enteros tiene como elemento neutro el 1
-10 . 1 = -10
126 . 1 = 126

