Para el estudio de la geometría es necesario saber, conocer y comprender muchas de sus definiciones, pero para comenzar a desarrollar la geometría, debemos tener bien claro estos fundamentos, son aquellos que se aceptan sin una definición previa como los elementos básicos de la geometría punto, recta y plano.
Por eso vamos a ver cómo se comportan y relacionan entre ellos.
También te puede interesar:
Donde surge la geometría
Uso de la geometría en la vida diaria
¿Qué es el plano?
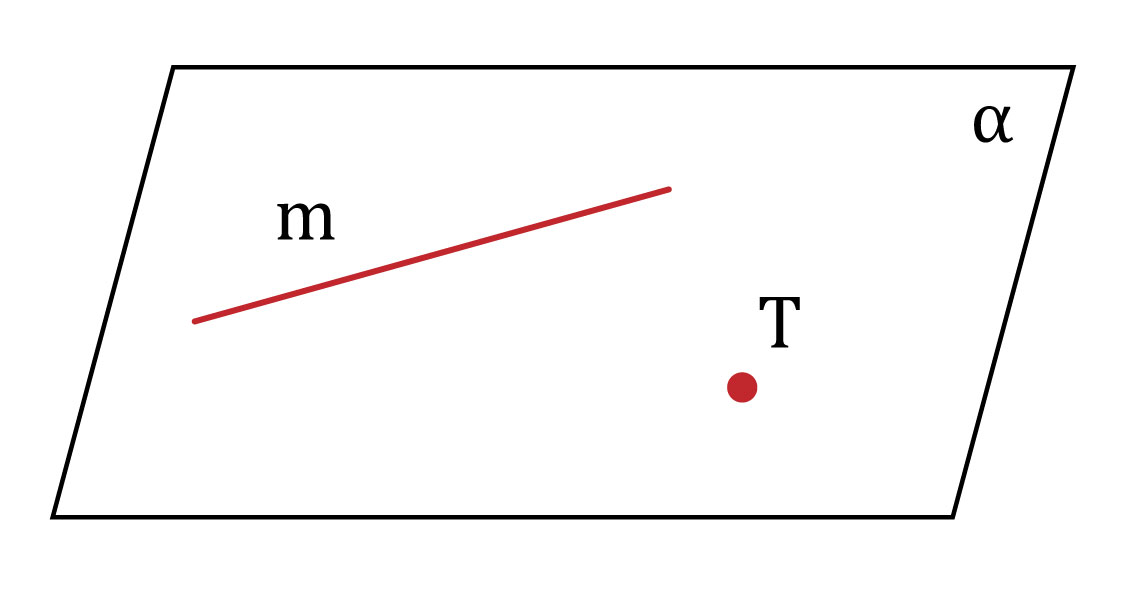
Es el conjunto de puntos que forman un espacio, el cual está dado de dos dimensiones. El plano normalmente está designado con una letra del alfabeto griego.
¿Qué es la recta?
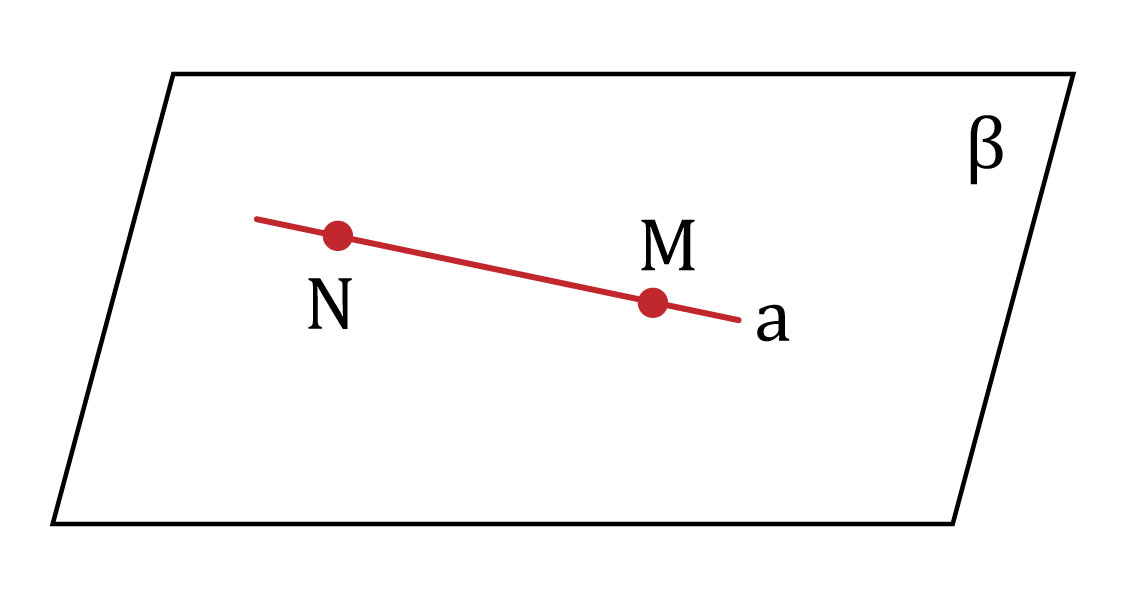
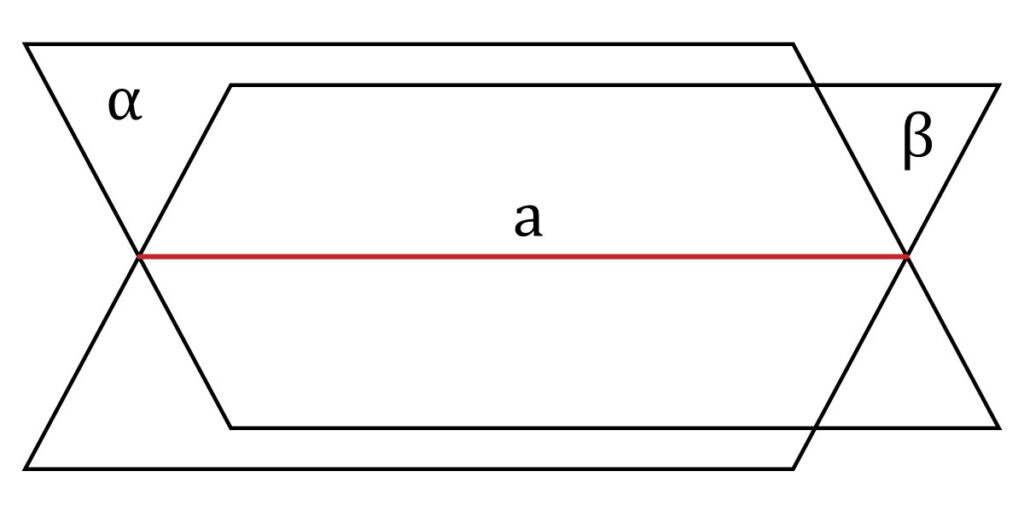
Es cuando se interceptan dos planos y forman un conjunto de puntos en la que se crea un espacio de una dimensión. Se designa con una letra minúscula del alfabeto.
El plano 
interceptado con el plano 
determina la recta a. 
¿Qué es el punto?
Es la intersección de dos rectas. Se designan con letras mayúsculas. La resta a interceptada con la recta b, determina el punto P. 
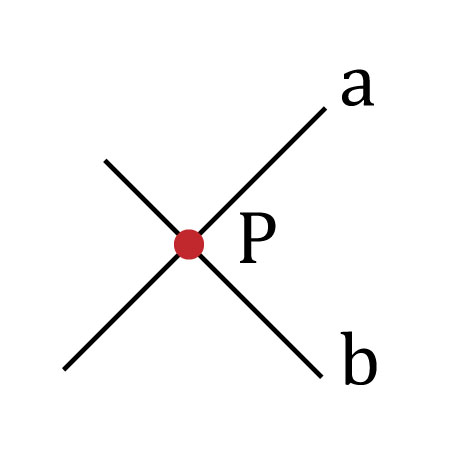
Los puntos, rectas y planos deben satisfacer ciertas propiedades que son aceptadas sin ningún tipo de demostración, la cual surgen de la observación y la experiencia.
Veamos unos postulados o axiomas:
- Existen infinitos puntos, infinitas rectas e infinitos planos.
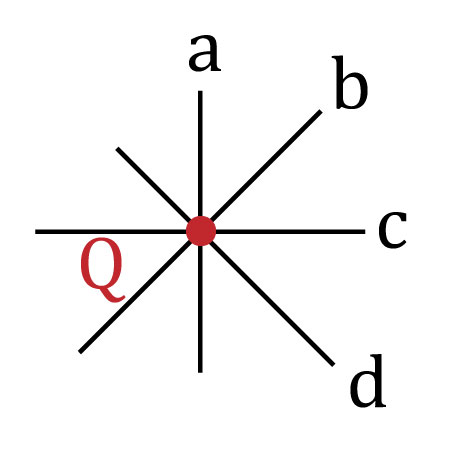
- Por un punto pasan infinitas rectas.
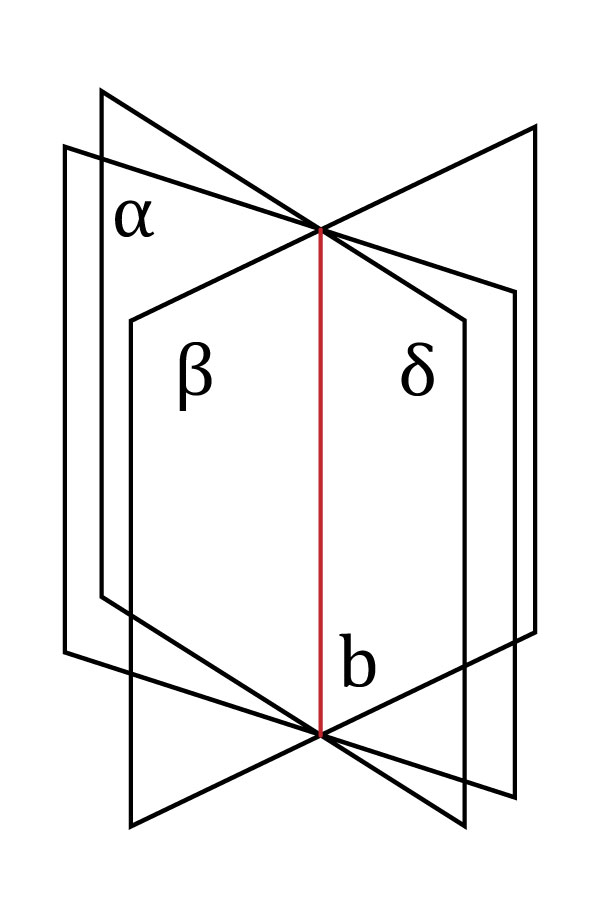
- Por una recta pasan infinitos planos.
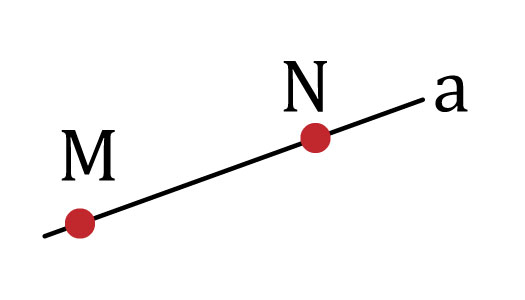
- Dos puntos determinan una recta en la que pertenecen.
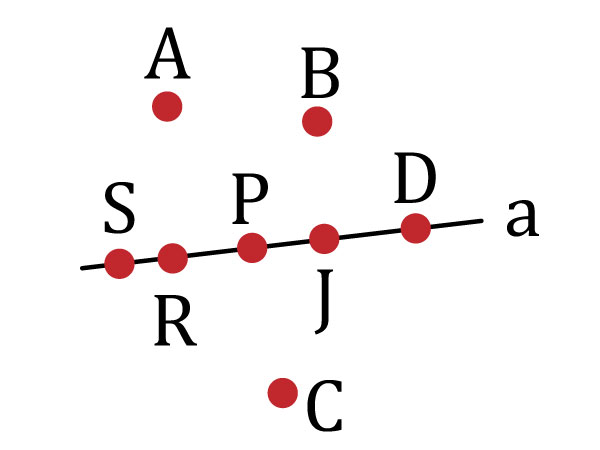
- Existen infinitos puntos que pertenecen a una recta y existen infinitos puntos que no pertenecen a ella.
- Una recta y un punto fuera de ella determina un plano, tanto la recta como el punto están incluidos en el plano.
- La recta determinada por dos puntos de un plano está incluida en dicho plano.
- Existen infinitos puntos dentro de un plano y existen infinitos puntos fuera de él.
